This lesson can be skipped if your only concern is with personality modeling, because my Bound Number Mathematics system handles all personality model calculations. However, the methods described here have broad applicability to many other problems and so might be of some value.
Comprehending math
There’s a big difference between passing a math course and actually understanding math. I have never met a computer person who understands simple math well enough apply it effectively. I earned a master of science degree in physics. In doing so, I passed courses in calculus, differential equations, probability and statistics, mathematical methods in the physical sciences, and even group theory. Yet when I began using math in my programming, I quickly realized that I did not understand how to actually apply mathematical operations to programming problems. It took me years to grasp some basic principles.
The problem here is the difference between theory and application. For example, I took a course in upper division electronics. I learned all sorts of interesting theory, such as Thevenin’s Theorem and Kirchoff’s Laws. Yet, some years later, when I had to build some actual circuits, I hadn’t the foggiest idea of how to proceed. Of course, the course I took was never intended to teach me how to build circuits; it was a physics course, fer cryin’ out loud! Still, this illustrates the problem. Sure, you took all sorts of math courses—but don’t think that you learned anything about how to actually use math in programming. Math theory and math application are entirely different subjects.
One-bit logic corresponds to multi-bit arithmetic
Let’s start with a simple truth that few programmers know: logical OR is just one-bit addition, and logical AND is just one-bit multiplication. That’s best appreciated by examining the truth tables for the operators:
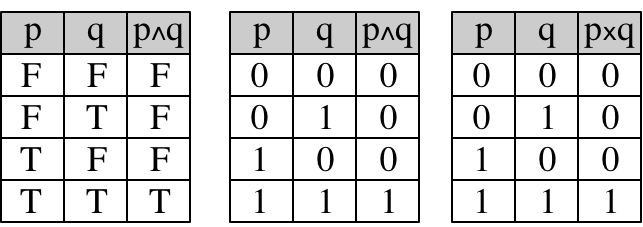
On the left, we have the standard truth table for the AND operator. In the center, we replace the T/F notation with 1/0. On the right, we show the table for multiplication. Voila! They’re the same!
The relationship between the logical OR operator and addition is a bit stickier, because 1+1=2, but if you’re willing to accept some hand-waving and smoke and mirrors on my part, I think you’ll agree to be convinced:

This leads to a simple rule of thumb: if you’re trying to figure out whether to use addition or multiplication, ask yourself, “Do I need BOTH of these two factors to get a big result, or can a big value of one compensate for a small value of the other?” In the former case, use multiplication; in the latter case, use addition.
An example: mom and supermom
Here’s an example of how we apply this thinking. The situation: Robbie the Teenager is working on his car (true, kids today don’t much work on cars, but suppose that this is the 1950s). He’s underneath the car when the jack fails and the car slides down on Robbie. It doesn’t kill him outright, but he’s definitely in trouble. He calls out for help.
Robbie’s mom hears his cries and rushes into the garage. She attempts to lift the car so that Robbie can escape from underneath it. You might think that the only factor determining her success in lifting the car will be her physical strength, but sometimes humans can summon astounding strength when they’re sufficiently motivated. So we should combine those two factors to determine Mom’s success: her physical strength and her motivation. The question is, how do we combine them? Do we add them together, or do we multiply them together? Apply Crawford’s Rule of Thumb:
“Do I need BOTH of these two factors to get a big result, or can a big value of one compensate for a small value of the other?”
Would Arnold Schwarzenegger be able to lift the car if he had zero concern for Robbie? Would Robbie’s mom be able to lift the car if she had zero strength (she’s a paraplegic)? It’s pretty clear that in both such cases, the car would not be lifted, even though Arnold is immensely strong and mom is immensely motivated. Thus, we conclude that you need BOTH motivation and strength to lift the car; we must therefore multiply the two values together to determine the chances that the car can be lifted.
A small point: don’t worry about subtraction and division; they’re just backwards versions of addition and multiplication. Anything you want to do with subtraction or division can be done with addition or multiplication; just reverse things.
Using Variance in Addition and Multiplication
Here’s another example of the uses of addition and multiplication. Suppose that you’re the producer for a big game project. You have a budget of $1 million. Let’s say the two primary sections of your budget are cosmetics (sound, music, graphics, and animation) and gameplay algorithms. You’ve budgeted $900,000 for cosmetics and $100,000 for algorithms. The game is about halfway through production. The boss comes to you and says that marketing is excited about the game and therefore they are adding $100,000 to your budget. How do you allocate the additional money between cosmetics and algorithms?
More money buys better quality. But the overall quality of the product depends upon some combination of the quality of the cosmetics and the quality of the algorithms. Of course, that combination will be complicated, but let’s start with the simplest assumption: that it is either the sum or the product of the qualities. Which of these two equations is closer to the truth:
Game quality = cosmetics quality + algorithm quality
Game quality = cosmetics quality x algorithm quality
If the upper equation seems right to you, then it doesn’t matter where you put the money. But if the lower equation seems right, then you definitely want to put all the additional money into the algorithm work, because doubling the algorithm quality will have a greater effect than increasing the cosmetics effect by 11%.
This analysis is wildly oversimplified. I can think of many ways to make it more complicated, and I’m sure that you can, too. The lesson here is not about game budgets; it’s about the fact that multiplication and addition have very different yet comprehensible effects on calculations. You must UNDERSTAND addition and multiplication if you wish to use them!
Using division safely
Sometimes you’ll want to use division, but you know that you run the risk of getting a divide by zero error. No problem! Just add something to the denominator, like so:
Output = x /(y+1)
Of course, this works only if y>0. If y<0, then you’ll be in a world of pain. Be careful!
More advanced mathematical operators
In general, you really don’t need to go much further than addition and multiplication. First, it’s a good idea to master addition and multiplication before moving on to, say, partial differential equations. Second, your competition still can’t hack addition and multiplication, so you can rule the world with merely a solid grasp of these two operators. Third, game design is still in a primitive stage; you don’t need a Saturn V rocket to get a gallon of milk at the grocery store.
Still, there are a few cases where slightly more powerful operators might be useful. Here’s how to think about using them.
In general, you have some sort of input and you want to get some sort of output. Think in terms of an amplifier. You have input (the microphone) and output (the speaker). You need to tune that amplifier to give you appropriate speaker output for the kinds of inputs you expect. You want a whisper to come across faintly in the speaker, and a shout to be loud but not deafening. You need to tune the responsiveness curve for the amplifier. Now, in general, you would want a nice linear responsiveness curve, like this:
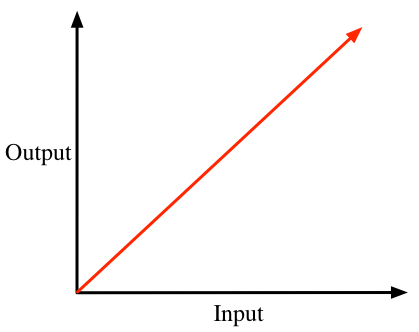
In a case like this, you don’t have to do any work; your equation is:
Output = Input
But you seldom get it this easy. Sometimes your input values are tiny and need to be amplified:
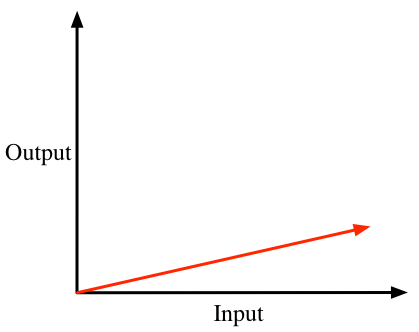
The input is tiny and you need much bigger output. This too is easy:
Output = a x Input
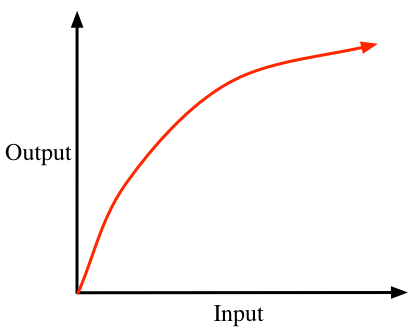
You just use a multiplier (a) greater than 1. This is still a ridiculously easy situation. Sometimes you’ll have reverse situation where the blue line shoots straight up; again, this is simple; you need merely muliply it by a number less than 1. But things start getting messy when the input is curvy:
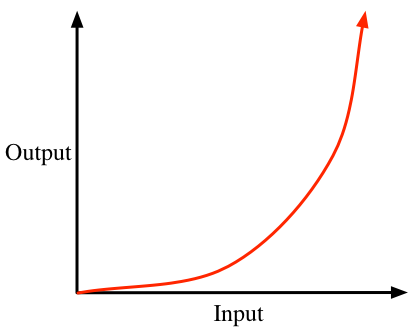
Situations like this need to be tamed. The simplest taming operator is the square root; it reduces the curvature of the red line.
Output = Sqrt(Input)
It might not be enough; in which case you have to take sterner action and use the log operator:
Output = log(Input)
You can add multipliers to these equations to scale the response to what you want.
The opposite extreme is the curve with a negative second derivative (don’t panic: that’s just calculus-talk):
You can straighten this curve out by squaring:
Output = Input x Input
If that’s not enough, then you can get really tough with exponentiation:
Output = 10**Input
More advanced operators
You won’t need anything else. Sure, you might need to use trig functions for geometrical applications. But I have only rarely had to use anything more advanced than the operators I use here. I’d guess that I do about 95% of all my work with just addition and multiplication. Squares and square roots take up maybe another few percentage points, and logs and exponentiation are quite rare.
Someday, when designers have learned how to actually use math in their designs, you may well end up using Fourier transforms, Legendre polynomials, and Gaussian functions. But that day is a long way off. Make sure you’ve got addition and multiplication down pat before you try anything fancy.
How to create algorithms
Here’s a simple way to create algorithms for dramatic interaction; it requires eight steps:
1. Write down, in plain English, a statement of the situation.
2. Write down, in plain English, what question you desire the algorithm to answer.
3. Write down, in plain English, the general principle that will determine the answer.
4. Identify and name the variables for the algorithm.
5. Express the general principle from above in boolean terms.
6. Convert the boolean form to numeric form.
7. Test your algorithm with a wide range of input values.
8. Adjust the algorithm to suit your artistic sensibilities.
Let’s walk this through an example.
Step1: State the situation

Frodo has finally gotten inside Mt. Doom and is ready to drop the Ring into the lava.

But the Ring tempts him.
Step 2: What is the question I want to answer?
Will Frodo keep the Ring?

Step3: State the general principle that will decide the answer
If Frodo is virtuous enough, or has enough willpower to overcome the Ring’s power, then Frodo will destroy the Ring.
Step 4: Identify and name the variables for the algorithm
Frodo’s Virtue
Frodo’s Willpower
Ring’s Power
Frodo_destroys_Ring
Step 5: Express the general principle in boolean terms
Frodo_destroys_Ring = Frodo’s Virtue OR Frodo’s Willpower is greater than the Ring’s Power
Step 6: Convert the boolean form to numeric form
Frodo_destroys_Ring = Frodo’s Virtue + Frodo’s Willpower > Ring’s Power
Step 7: Test your algorithm with a wide range of input values.
Step 8: Adjust the algorithm to suit your artistic sensibilities.
Hmm… I think that Frodo’s willpower should play a larger role in the decision than his virtue. Therefore, I’ll double the importance of his willpower, like so:
Frodo_destroys_Ring = Frodo’s Virtue + 2 * Frodo’s Willpower > Ring’s Power
However, you might disagree; you might well judge that virtue is more important than willpower. That’s an artistic decision, not a technical decision. This is where the art enters the process. Indeed, of the eight steps in this process, there are more artistic judgements than technical judgements:
Artistic: 1. Write down, in plain English, a statement of the situation.
Artistic: 2. Write down, in plain English, what question you desire the algorithm to answer.
Artistic: 3. Write down, in plain English, the general principle that will determine the answer.
Artistic: 4. Identify and name the variables for the algorithm.
Technical: 5. Express the general principle from above in boolean terms.
Technical: 6. Convert the boolean form to numeric form.
Technical: 7. Test your algorithm with a wide range of input values.
Artistic: 8. Adjust the algorithm to suit your artistic sensibilities.
