A fascinating theoretical problem is posed by the choice between color and resolution in screen design. We all prefer, of course, to use as many colors and as much resolution as possible, but in a world of finite resources, we must choose. The current choice is between the two best display modes of a VGA board: 640 x 480 x 4 bits and 320 x 200 x 8 bits; but there are other options as well and we can be certain that, while the exact parameters may change, the basic choice between resolution and color will remain with us for awhile.
Subjectivity versus Objectivity
I shall begin my analysis with a few snide remarks at the anarchic position. This school argues that it’s all utterly subjective and that therefore there can be no rational basis for making a choice. A black & white drawing by Michaelangelo surpasses a multi-colored crayon piece by a four-year-old. (To which another anarchist might reply, "Who said Michaelangelo is better than a four-year-old?")
This school confuses the instance with the principle. It sees everything in terms of individual items rather than statistical ensembles. I readily concede that any individual image might be better or worse than any other individual image, but I am talking in statistical terms. In general, all other things being equal, will a higher-resolution image be better than a higher-color image? To put it another way: if we were to gather a thousand representative high-resolution images, and a thousand high-color images, would we be able to make an overall statement as to their relative collective quality?
There really is such a thing as objective truth, even in matters of aesthetic. The objective dimension of the arts lies in the physical mechanics of human perception. We may argue endlessly and futilely whether Beethoven is better than Bo Diddley, but there can be no arguing that a CD presents the music better than an analog Philips casette. The human ear is capable of perceiving sounds in a certain range; the fraction of that range that a musical medium can capture, and the fidelity with which it does so constitutes an objective measure of the quality of the medium.
The same thing is true of the human eye. The eye is not a linear transducer; it is a vastly complex organ whose response to visual stimuli is still the object of scientific research. For example, we know that the eye has a particularly strong response to scenes with large spatial or temporal derivatives (i.e., sharp edges or fast motion.) There are also many indications that the eye is not two-dimensionally uniform: its side-to-side perception differs from its top-to-bottom perception. Moviemakers know this: that’s why movie screens are wide and short.
Artists as Sources of Information
This last observation regarding movie screens suggests a novel strategy for learning about the characteristics of the eye. Do you think that movie moguls hired a bunch of perceptual psychologists and asked them to determine the optimal dimensions of a movie screen? I doubt it. My guess is that the dimensions of the movie screen arose from the urgings of the directors and cinematographers -- the artists. They may not have any formal training in physiology, but they have innate knowledge of how the human visual system works.
This suggests to me that we might be able to learn a thing or two about the human eye by examining the work of artists. We must be careful to look at many artists, to statistically compile a great deal of work, for artwork is so idiosyncratic that we could easily fall prey to errors if our sample were too small. In order to explain the next step in my reasoning, I must now step aside and take a circuitous digression. Bear with me.
Information Content
The amount of information in an image is simply the number of pixels multiplied by the number of bits per pixel. Thus, a 320 x 200 x 4 bit image will require 32,000 bytes to display. A 640 x 480 x 8 bit image will require 307,200 bytes. But this calculation does not reveal the information content of the image, only its information capacity -- how much information it could optimally convey. I could present you with a 640 x 480 x 8 bit image that contains, in 72-point text, the single word "Hi". Although my computer would require 307,200 bytes to present you with that image, the amount of genuine information in that image is far less that 307,200 bytes. This is true of all images. Every image falls short of its medium in that it cannot possibly utilize every ounce of information capacity. Thus, we seem to be stuck. We cannot measure the actual information content of any image, only its information potential, how much information it might convey if it were a perfect (whatever that is) image.
Now, you might be wondering what significance this has. Who cares about information content or information potential? My answer is sweet and pithy: truth is beauty. I assert that information (truth) is intrinsically beautiful. The more information content an image presents, the more visual substance it has, the more it delights the eye. An image of random pixels is not beautiful, because it has no information content. An image of uniform color is also not beautiful, because it too has no information content. But if the image is organized, if it has elements that fit together, suggesting meaning, then it has information content -- and beauty. Our problem is, how can we measure the information content?
Measuring Information Through Compression
How efficient is English as a medium for conveying information? The answer lies in text compression. English uses 26 letters in its alphabet. Ideally, each letter would be used with equal frequency, but we know that is not the case. Some letters -- q, x, and z, for example -- are used rarely, while others -- e, t, and i -- are used heavily. This manifests itself in high compression factors for English ASCII text. If you take some English text in ASCII form and compress it with a file compressor, you will get a file that is perhaps only 35% of the size of the original. This 35% figure I will refer to as the compression factor.
The compressed filesize is a measure of the true information content of any expression. In other words, if you take a raw textfile, image, or sound, and measure the size of the file, you do not necessarily have a reliable measure of the information content of the expression. The image could be a screen dump of a blank white screen, yet still consume 307,200 bytes. The sound could be 10 seconds of silence at 22 KHz sampling rate, yet would still eat up 220K of space. However, if you compress that sound file with a competent compressor, it will squeeze down to almost nothing, which is a much better statement of its information content. If you compress the blank white screen, it too will shrink to almost nothing in size. Thus, the compressed filesize is a measure of true information content.
So here we have a tool for measuring the information content of our images. Suppose we measure the information content of many actual game screen images. We cannot directly compare information content, for that depends on image size. But we can directly compare the compression factors. If we discover that these compression factors are higher for 4-bit images than for 8-bit images, then we can conclude that artists are able to squeeze more information content into those 4-bit images.
A Test Drive with Font Sizes
As a simple test of the basic principle, I carried out a somewhat different test. I set up a large essay in MicroSoft Word, formatted in 9-point text. Then, using a screen dump utility, I captured the image of the text window as a straight bitmap. I compressed this bitmap and recorded its file size. Then I returned to MicroSoft Word and reformatted the text to 10 points. Once again I captured the image -- but I captured the same window, not the same text. Because the text was larger, I captured fewer characters even though I captured the number of pixels. Again, I compressed the resulting bitmap and recorded its file size. Then I repeated this process for other text sizes and for another font. The results:
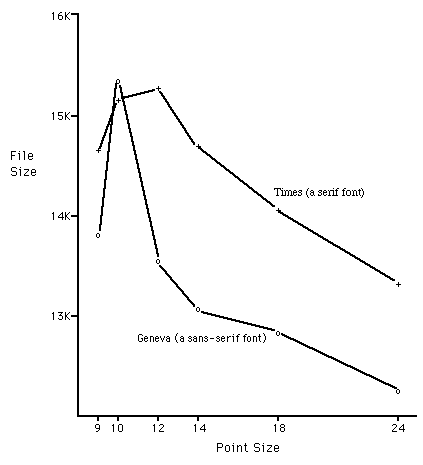
This graph clearly shows that information content is highest with the 10-point Geneva font and the 12-point Times font. It should come as no surprise that these two sizes are the most popular sizes for word processing on the Macintosh screen. However, the reader might wonder why the graphs peak. As the font grows smaller, we pack more pixels onto the screen. Shouldn’t the graph continue to rise as we move from larger point sizes to smaller point sizes?
The answer lies in the artists who designed the fonts. They realized that the tiny fonts were hard to read, so they inserted additional leading (white space between lines of text) to make it easier for the eye. From 24 points down to 12 points, the lines are packed together with minimal leading, but below 12 points the additional leading takes its toll on information content.
This little excursion shows how the information content analysis can be used to discover artistic truths that are otherwise hard to make explicit. Every Macintosh user knows that the 10-point and 12-point font sizes are the best sizes to use, but if you demand to know why this is so, the user will glance about helplessly and shrug, "It just looks better." This graph shows why.
The Screen Image Data
Aaron Urbina and I captured a total of 47 different screen images from 13 different games. There were Macintosh games and IBM games, games with 1-bit, 4-bit, and 8-bit graphics. We exercised some judgement in the images we chose. For example, we excluded games with emphasis on fast animation (mostly skill & action games and flight simulators) because such games often require simple backgrounds, and such simple (i.e., low information content) backgrounds would bias the sample. We also excluded images from such games as Loom and Balance of the Planet, because both products made deliberate use of very clean, simple graphics styles. Again, this would have biased the data. For opposite reasons, we ruled out scanned photographic images. Finally, we excluded screen images that contained mostly text. We concentrated our attention on games with extensive hand-drawn artwork; I believe that such screen images come closest to satisfying the reasoning presented earlier in this essay.
The resulting compression factors are presented in graphical form:
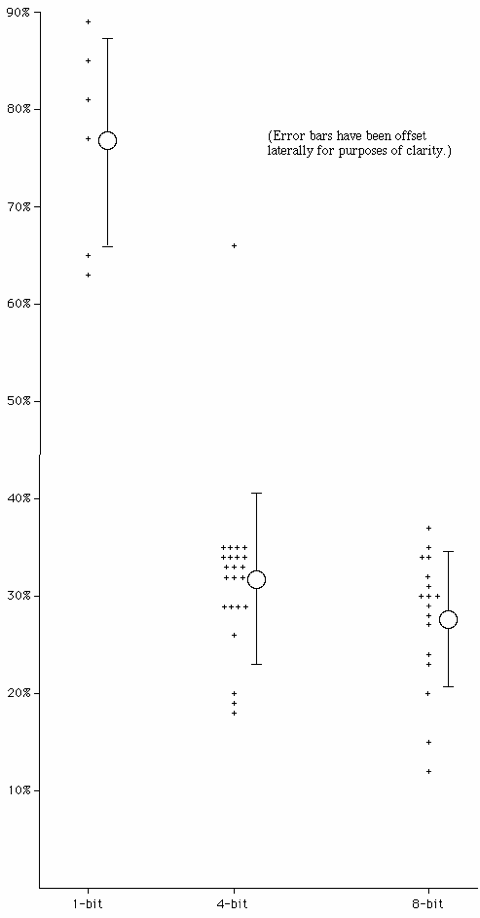
What does this mean? My analysis of this graph is complicated. My first consideration is with the unavoidable sources of error -- they are subtle and significant. One such is the fact that most of the 4-bit data comes from games that are older than those providing the 8-bit data. The significance of this lies in the fact that the cost per bit of storing data on floppy disks has fallen rapidly. Thus, much of the 4-bit imagery was created at a time when publishers were more sensitive to the production costs of large, elaborate imagery, and so tended towards simpler images. The 8-bit data, being more recent, should be less sensitive to this concern. The upshot of this is that the 4-bit data is pushed towards lower compression factors relative to the 8-bit data. To put it bluntly: the 4-bit data is probably lower than it should be.
Another problem arose from the intermixture of text and graphics. Almost all game screens mix the two, but how much text can I accept and still have a valid test of a hypothesis whose primary concern lies with graphics? This is a really tough issue, because text is just as important as graphics. Every game has some text, yet text tends to bias this analysis towards resolution instead of color. You only need two colors to show text foreground and background but you need as many pixels as you can get for good resolution. Moreover, restricting the data sample to images that contain no text whatsoever would drastically reduce my sample size. I decided to reject screen images that are primarily text, and to accept any image with more than about 50% of its space devoted to graphics. I could argue that this deliberate exclusion of a significant portion of the screens from real-world games biases my results against resolution, but in the end I decided to err in the direction of conservatism.
Another potential source of error arises from the compression overhead. Most compressors have a certain amount of overhead. The filesize is equal to some constant (the overhead) plus the actual information content. I examined the effect of this problem by starting with a large 16-color image (the map from Patton Strikes Back), compressing it into a GIF file, calculating its compression factor, and then repeating the process for smaller chunks taken from the same image. I present the results in tabular format:
| Buffer Size | GIF Size | Compression Factor |
| 144,000 | 100,279 | 68% |
| 46,200 | 31,589 | 68% |
| 20,400 | 13,846 | 70% |
| 6,400 | 4,470 | 70% |
| 5,600 | 3,693 | 66% |
If the overhead were a significant factor in this analysis, then the compression factor would increase as the buffer size decreased. This does not appear to be the case. I conclude that overhead is not a significant consideration.
Conclusions
It’s clear that 1-bit images have far more information content than either the 4-bit or the 8-bit images. We get more bang for our buck, more picture for our pixels, with black and white images than with color images. I think this is because the choices an artist faces with a black and white image are simpler than those with a color image. An artist decides only whether a given pixel should be black or white. This simpler level of decision-making encourages, I think, a greater expenditure of artistic effort on each pixel. Artists can afford to lavish more attention on black and white images -- and they must do so if they are to obtain decent results. The result is that, pixel for pixel, black and white images carry more visual punch, more information content, than color images.
The situation with color images is not so clear. If we compare the 4-bit results with the 8-bit results alone, we discover that the difference is not statistically significant. There is no statistical basis, from the 4-bit results and the 8-bit results alone, to say that 4-bit images have more information content than 8-bit images.
However, the strong showing of the 1-bit results cannot be ignored. If we do a linear analysis on all three bit depths, then we get a significant difference. There really is something going on here: that graph is too steep to dismiss. When we recall that the primary sources of error tend to push the 4-bit data downward, I think it safe to say that the initial hypothesis is probably confirmed. At the levels of resolution and color with which we work, resolution is more informative than color. 4-bit images communicate more to players than 8-bit images.
As times change, this conclusion will lose its force. As we move to higher resolutions with SVGA and other displays, the value of color will rise. The difference between 4-bit images and 8-bit images is already small; I expect it to disappear as we make the next step upwards in resolution.
